Algoritmo 7 – Estado de Bell

A interação entre os qubits de um circuito quântico pode resultar em um estado quântico emaranhado conhecido como estado de Bell. Nesse estado, o estado quântico de cada qubit não pode mais ser descrito independentemente. O estado emaranhado representa o sistema como um todo e o que ocorre em um qubit afeta os outros qubits do circuito. Para gerar um estado emaranhado, pode-se utilizar um circuito quântico com dois qubits, uma porta de Hadamard e uma porta CNOT. A porta de Hadamard é aplicada sobre o primeiro qubit que servirá como qubit de controle para a porta CNOT, que terá o segundo qubit como qubit alvo. A Figura 1 mostra o circuito quântico associado ao algoritmo 7 desse tutorial.

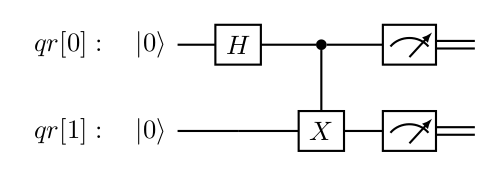
Figura 1. Circuito quântico que produz um sistema em um estado quântico de Bell.

O estado do primeiro qubit é descrito por $\left| \psi_{1} \right\rangle = \alpha \left| 0 \right\rangle + \beta \left| 1 \right\rangle$ e o estado do segundo qubit por $\left| \psi_{2} \right\rangle = \gamma \left| 0 \right\rangle + \delta \left| 1 \right\rangle$. A superposição desses dois estados resulta no estado $\left| \psi \right\rangle = \alpha \gamma \left| 00 \right\rangle + \alpha \delta \left| 01 \right\rangle + \beta \gamma \left| 10 \right\rangle + \beta \delta \left| 11 \right\rangle$. Esse estado deve ser igual ao estado gerado pela ação da porta de Hadamard seguida pela porta CNOT que é o estado $\left| \psi \right\rangle = \left( \left| 00 \right\rangle + \left| 11 \right\rangle \right)/\sqrt{2}$. Porém, não é possível obter uma solução para a equação:

$$ \alpha \gamma \left| 00 \right\rangle + \alpha \delta \left| 01 \right\rangle + \beta \gamma \left| 10 \right\rangle + \beta \delta \left| 11 \right\rangle = \left(\left| 00 \right\rangle + \left| 11 \right\rangle \right)/\sqrt{2}$$

Portanto, o estado emaranhado é um estado que não deveria existir. Experimentos recentes têm encontrado evidências de estados emaranhados de fótons e elétrons. Temos a seguir, os algoritmos que implementam o circuito quântico da Figura 1 para os SDKs Qiskit, Forest e Cirq.

Qiskit

Para implementar o circuito quântico da Figura 1 utilizando o SDK Qiskit, é necessário as bibliotecas QuantumCircuit, QuantumRegister, ClassicalRegister, Aer e execute. Essas bibliotecas são importadas pelos mesmos comandos utilizados no algoritmo anterior. Devem ser instanciados dois registradores quânticos e dois clássicos. Logo, as linhas de comando que devem ser inseridas no programa são:
qr = QuantumRegister(2)
e
cr = ClassicalRegister(2).
O circuito quântico é instanciado por:
qc = QuantumCircuit(qr,cr).
A porta de Hadamard e a porta CNOT são implementadas no circuito por:
qc.h(qr[0])
e
qc.cx(qr[0],qr[1]).
O circuito é finalizado com os medidores que são implementados no algoritmo por:
qc.measure(qr[0],cr[0])
e
qc.measure(qr[1],cr[1]).
O simulador a ser utilizado é o QASM Simulator que é selecionado por:
backend = Aer.get_backend('qasm_simulator').
Os comandos para a execução do algoritmo são os mesmos discutidos no algoritmo 1. O algoritmo 7 completo para o SDK Qiskit é mostrado a seguir:

from qiskit import QuantumCircuit
from qiskit import QuantumRegister
from qiskit import ClassicalRegister
from qiskit import Aer
from qiskit import execute
qr = QuantumRegister(2)
cr = ClassicalRegister(2)
qc = QuantumCircuit(qr,cr)
qc.h(qr[0])
qc.cx(qr[0],qr[1])
qc.measure(qr[0],cr[0])
qc.measure(qr[1],cr[1])
backend = Aer.get_backend('qasm_simulator')
job = execute(qc,backend,shots=100)
resultado = job.result()
contagem = resultado.get_counts()
print(contagem)

Como foi atribuído o valor 100 à variável shots, são realizadas cem medições que resultam em 00 ou 11. A probabilidade de obter o resultado 00 em um processo de medição é $\left| 1/\sqrt{2}\right|^2$ = 0,5. Essa é a mesma probabilidade de obter o resultado 11. Um dos possíveis resultados obtidos na execução do algoritmo acima é {'11': 52, '00': 48}. Outro resultado possível seria {'11': 44, '00': 56}.

Forest

No Forest, as bibliotecas necessárias para a execução do algoritmo 7 são importadas pelos comandos:
from pyquil import get_qc, Program,
from pyquil.gates import *
e
from pyquil.quilbase import Declare.
O circuito quântico é instanciado por:
p = Program().
A porta de Hadamard e a porta CNOT são implementadas no circuito por:
p += H(0)
e
p += CNOT(0,1).
Os dois registradores clássicos necessários para armazenar os dados das medições realizadas são instanciados por:
ro = p.declare('ro', 'BIT', 2).
Os medidores quânticos são implementados por:
p += MEASURE(0, ro[0])
e
p += MEASURE(1, ro[1]).
O maior número de execuções é determinado pelo método wrap_in_numshots_loop(). A máquina quântica virtual para dois qubits é instanciada por:
qc = get_qc("2q-qvm").
O programa é compilado pelo método compile() e executado pelo método run(). O algoritmo 7 completo é mostrado abaixo.

from pyquil import get_qc, Program
from pyquil.gates import *
from pyquil.quilbase import Declare
p = Program()
p += H(0)
p += CNOT(0,1)
ro = p.declare('ro', 'BIT', 2)
p += MEASURE(0, ro[0])
p += MEASURE(1, ro[1])
p.wrap_in_numshots_loop(10)
qc = get_qc("2q-qvm")
executable = qc.compile(p)
result = qc.run(executable)
print(result.readout_data.get('ro'))

O resultado que deve ser obtido com a execução desse algoritmo é:
[ [0 0]
  [1 1]
  [0 0]
  [1 1]
  [0 0]
  [1 1]
  [1 1]
  [1 1]
  [1 1]
  [0 0] ]

Como explicado anteriormente, no Forest, obtemos os resultados das medições realizadas em uma matriz. Cada linha dessa matriz contém um elemento que armazena os resultados das medições realizadas em uma execução do algoritmo. Como foram executadas duas medições em cada execução, temos dois resultados em cada elemento dessa matriz. O primeiro valor corresponde ao resultado da medição do qubit qr[0] e o segundo valor, ao resultado da medição do qubit qr[1]. O resultado [1 1] corresponde ao resultado qr[0] = 1 e qr[1] = 1, que foi obtido seis vezes, e o resultado [0 0] corresponde ao resultado qr[0] = 0 e qr[1] = 0, que foi obtido quatro vezes. Em qualquer medição, a probabilidade de obter o resultado [1 1] é 0,5 e a probabilidade de obter o resultado [1 1] também é 0,5.

Cirq

Para implementar o circuito quântico da Figura 1 usando o SDK Cirq, deve-se importar a biblioteca cirq através de
import cirq.
Então, instancia-se o circuito quântico por
qc = cirq.Circuit().
Os dois qubits necessários no circuito são implementados no circuito por:
qr0 = cirq.NamedQubit('qr[0]')
e
qr1 = cirq.NamedQubit('qr[1]').
Sobre o qubit qr[0] deve ser aplicada uma porta de Hadamard por:
qc.append(cirq.H(qr0)).
A porta CNOT é adicionada ao circuito por:
qc.append(cirq.CNOT(qr0,qr1)).
As medições dos qubits são realizadas por:
qc.append(cirq.measure(qr0,key = 'qr[0]'))
e
qc.append(cirq.measure(qr1,key = 'qr[1]')).
O simulador é instanciado por:
simulador = cirq.Simulator()
e o comando para executar o programa é:
resultado = simulador.run(qc,repetitions=10).
O algoritmo completo é mostrado a seguir:

import cirq
qc = cirq.Circuit()
qr0 = cirq.NamedQubit('qr[0]')
qr1 = cirq.NamedQubit('qr[1]')
qc.append(cirq.H(qr0))
qc.append(cirq.CNOT(qr0,qr1))
qc.append(cirq.measure(qr0,key = 'qr[0]'))
qc.append(cirq.measure(qr1,key = 'qr[1]'))
simulador = cirq.Simulator()
resultado = simulador.run(qc,repetitions=10)
print(resultado)

Um exemplo de resultado para a execução desse algoritmo é:
qr[0]=0000011010
qr[1]=0000011010

No Cirq, os resultados de cada medição são apresentados em sequência após o sinal de igualdade que segue a variável que identifica o qubit medido. No resultado apresentado acima, a primeira medição resulta em 0 para qr[0] e 0 para qr[1]. A segunda, a terceira, a quarta, a quinta, a oitava e a décima medição também resultam nos mesmos valores para qr[0] e qr[1]. A sexta, a sétima e a nona medição resultam em 1 para qr[0] e 1 para qr[1]. A probabilidade para o resultado qr[0] = 0 e qr[1] = 0 é 0,5. Essa é a mesma probabilidade de se obter o resultado qr[0] = 1 e qr[1] = 1. Logo, qualquer combinação desses resultados é possível. Por exemplo, outro resultado possível seria:
qr[0]=1110001010
qr[1]=1110001010