Algoritmo 8 – Full Adder Quântico

O circuito quântico equivalente ao circuito lógico Full Adder pode ser construído com o uso de portas CNOT e TOFFOLI. As portas de Pauli X são utilizadas para modificar os estados iniciais dos qubits para obter os valores a serem somados. A figura abaixo mostra o circuito quântico Full Adder. Os qubits qr[0] e qr[1] armazenam os valores a serem somados. Na figura, uma porta de Pauli X foi aplicada ao qubit qr[0] para modificar o seu estado de $\left|0\right\rangle$ para $\left|1\right\rangle$ para que seja realizada a soma de 1 e 0. O qubit qr[2] equivale ao bit carry in e o qubit qr[3] equivale ao bit carry out. Outra porta de Pauli X foi aplicada ao qubit qr[2] alterando o seu estado inicial para $\left|1\right\rangle$. Assim, esse circuito realizará a soma de 1 e 0 com carry in igual a 1. O resultado dessa soma deve ser 2. Para obter o resultado, os qubits a serem medidos são qr[2] e qr[3] e os valores medidos devem ser 0 e 1, respectivamente.

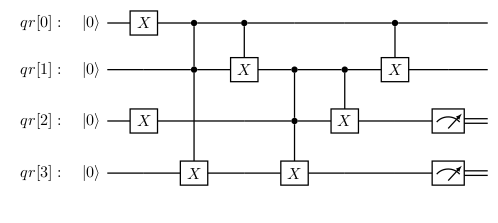
Figura 1. Full Adder Quântico.

Qiskit

Inicia-se o algoritmo com a importação das bibliotecas: QuantumCircuit, QuantumRegister, ClassicalRegister, Aer e execute. São necessários quatro qubits que devem ser instanciados por:
qr = QuantumRegister(4).
Os resultados das medições dos qubits qr[2] e qr[3] devem ser armazenados em dois registradores clássicos instanciados por:
cr = ClassicalRegister(2).
O circuito quântico é instanciado por:
qc = QuantumCircuit(qr,cr).

Os qubits qr[0] e qr[2] devem ter seu estado alterado de $\left|0\right\rangle$ para $\left|1\right\rangle$. Para isso, portas de Pauli X são aplicadas sobre esses qubits através de:
qc = qc.x(qr[0])
e
qc = qc.x(qr[2]).
Aqui, os estados dos qubits são: qr[0] no estado $\left|1\right\rangle$, qr[1] no estado $\left|0\right\rangle$, qr[2] no estado $\left|1\right\rangle$ e qr[3] no estado $\left|0\right\rangle$. Então, adicionamos ao circuito uma porta TOFFOLI com os qubits qr[0] e qr[1] como qubits de controle e qr[3] como qubit alvo por meio do método:
qc.ccx(qr[0],qr[1],qr[3]).
O qubit qr[3] não tem o seu estado alterado. Uma porta CNOT é adicionada ao circuito por:
qc.cx(qr[0],qr[1]).
Essa porta tem qr[0] como qubit de controle e qr[1] como qubit alvo. Como o estado de qr[0] é $\left|1\right\rangle$, o estado de qr[1] é alterado para $\left|1\right\rangle$. Em seguida, adicionamos ao circuito a segunda porta TOFFOLI por:
qc.ccx(qr[1],qr[2],qr[3]).
Essa porta altera o estado de qr[3] para $\left|1\right\rangle$ porque tanto qr[1] quanto qr[2] estão no estado $\left|1\right\rangle$. Duas portas quânticas CNOT são implementadas no circuito por:
qc.cx(qr[1],qr[2])
e
qc.cx(qr[0],qr[1]).
A primeira altera o estado de qr[2] de $\left|1\right\rangle$ para $\left|0\right\rangle$ e a segunda altera o estado de qr[1] para $\left|0\right\rangle$. Então, adicionam-se os operadores que realizam as medições nos qubits qr[2] e qr[3] através de:
qc.measure(qr[2],cr[0])
e
qc.measure(qr[3],cr[1]).

O algoritmo é finalizado com os comandos:
backend = Aer.get_backend('qasm_simulator'),
job = execute(qc,backend,shots=100),
resultado = job.result(),
contagem = resultado.get_counts()
e
print(contagem).

O algoritmo 8 completo e sem interrupções é mostrado a seguir:

from qiskit import QuantumCircuit
from qiskit import QuantumRegister
from qiskit import ClassicalRegister
from qiskit import Aer
from qiskit import execute
qr = QuantumRegister(4)
cr = ClassicalRegister(2)
qc = QuantumCircuit(qr,cr)
qc.x(qr[0])
qc.x(qr[2])
qc.ccx(qr[0],qr[1],qr[3])
qc.cx(qr[0],qr[1])
qc.ccx(qr[1],qr[2],qr[3])
qc.cx(qr[1],qr[2])
qc.cx(qr[0],qr[1])
qc.measure(qr[2],cr[0])
qc.measure(qr[3],cr[1])
backend = Aer.get_backend('qasm_simulator')
job = execute(qc,backend,shots=100)
resultado = job.result()
contagem = resultado.get_counts()
print(contagem)

O resultado desse algoritmo será: {'10': 100}. Nas cem execuções foi obtido o resultado 10, ou seja, qr[3] = 1 e qr[2] = 0. O grande número de execuções mostra que esse é o único resultado que pode ser obtido, portanto a probabilidade desse resultado é 1. O resultado 10, que deve-se a 1 para o bit carry out e 0 para o bit de soma, equivale ao número decimal 2 em notação binária.

Forest

O algoritmo 8 para o SDK Forest inicia-se com a importação das bibliotecas necessárias para a execução do programa. Essas são as mesmas utilizadas no algoritmo anterior. Então, o circuito quântico é instanciado por:
p = Program().
Os qubits qr[0] e qr[2] têm os seus estados alterados pelas portas de Pauli X implementadas por:
p += X(0)
e
p += X(2).
A primeira porta TOFFOLI é implementada por:
p += CCNOT(0,1,3).
Essa porta quântica não altera o estado do seu qubit alvo. Em seguida, é adicionado ao circuito uma porta CNOT pela linha de comando:
p += CNOT(0,1).
A segunda porta TOFFOLI é adicionada por:
p += CCNOT(1,2,3).
As duas portas CNOT finais são implementadas por:
p += CNOT(1,2),
e
p += CNOT(0,1).

Os registradores clássicos são instanciados por:
ro = p.declare('ro', 'BIT', 2).
Esses registradores são necessários para armazenar os resultados das medições dos qubits qr[2] e qr[3] que foram medidos pelos medidores implementados por:
p += MEASURE(2, ro[0])
e
p += MEASURE(2, ro[0]).
As linhas de comando finais para a compilação e execução do algoritmo são as mesmas adicionadas no algoritmo anterior. O algoritmo completo é mostrado abaixo.

from pyquil import get_qc, Program
from pyquil.gates import *
from pyquil.quilbase import Declare
p = Program()
p += X(0)
p += X(2)
p += CCNOT(0,1,3)
p += CNOT(0,1)
p += CCNOT(1,2,3)
p += CNOT(1,2)
p += CNOT(0,1)
ro = p.declare('ro', 'BIT', 2)
p += MEASURE(2, ro[0])
p += MEASURE(3, ro[1])
qc = get_qc("4q-qvm")
executable = qc.compile(p)
result = qc.run(executable)
print(result.readout_data.get('ro'))

O resultado da execução do algoritmo acima é [ [0 1] ]. Esse resultado é expresso como uma matriz que contém um único elemento que é o par de valores 0 e 1. O valor 0 é o resultado da medição do qubit qr[2] e o valor 1 é o resultado da medição do qubit qr[3]. O qubit qr[2] equivale ao bit que contém o resultado da soma e o qubit qr[3] equivale ao bit de carry out. Logo, o resultado [ [0 1] ] equivale ao número binário 10 que é o número decimal 2.

Cirq

No Cirq, o algoritmo inicia-se com o comando para importar a biblioteca cirq:
import cirq.
Então, o circuito quântico e os quatro qubits são instanciados por:
qc = cirq.Circuit(),
qr0 = cirq.NamedQubit('qr[0]'),
qr1 = cirq.NamedQubit('qr[1]'),
qr2 = cirq.NamedQubit('qr[2]')
e
qr3 = cirq.NamedQubit('qr[3]').
As portas quânticas são implementadas no circuito pelo método append(). A sequência de comandos que implementam as portas quânticas do circuito são:
qc.append(cirq.X(qr0)),
qc.append(cirq.X(qr2)),
qc.append(cirq.TOFFOLI(qr0,qr1,qr3)),
qc.append(cirq.CNOT(qr0,qr1)),
qc.append(cirq.TOFFOLI(qr1,qr2,qr3)),
qc.append(cirq.CNOT(qr1,qr2))
e
qc.append(cirq.CNOT(qr0,qr1)).
Os medidores quânticos são implementados por:
qc.append(cirq.measure(qr2,key = 'qr[2]'))
e
qc.append(cirq.measure(qr3,key = 'qr[3]')).
O simulador é instanciado por:
simulador = cirq.Simulator().
O algoritmo é executado pelo método run() que é implementado por:
resultado = simulador.run(qc,repetitions=10).
O algoritmo completo é mostrado abaixo.

import cirq
qc = cirq.Circuit()
qr0 = cirq.NamedQubit('qr[0]')
qr1 = cirq.NamedQubit('qr[1]')
qr2 = cirq.NamedQubit('qr[2]')
qr3 = cirq.NamedQubit('qr[3]')
qc.append(cirq.X(qr0))
qc.append(cirq.X(qr2))
qc.append(cirq.TOFFOLI(qr0,qr1,qr3))
qc.append(cirq.CNOT(qr0,qr1))
qc.append(cirq.TOFFOLI(qr1,qr2,qr3))
qc.append(cirq.CNOT(qr1,qr2))
qc.append(cirq.CNOT(qr0,qr1))
qc.append(cirq.measure(qr2,key = 'qr[2]'))
qc.append(cirq.measure(qr3,key = 'qr[3]'))
simulador = cirq.Simulator()
resultado = simulador.run(qc,repetitions=10)
print(resultado)

O resultado da execução do algoritmo acima é:
qr[2]=0000000000
qr[3]=1111111111

Temos o mesmo resultado em todas as medições realizadas. Para o qubit qr[3], que equivale ao bit carry out, o valor é 1 e para o qubit qr[2], que equivale ao resultado da soma, o valor é 0. Esse resultado equivale ao número binário 10 que é o número decimal 2.