Algoritmo 3 – Porta de Pauli X

Algumas portas quânticas podem ser comparadas com portas lógicas como é o caso da porta de Pauli X que é comparada com a porta lógica NOT porque, quando a porta de Pauli X é aplicada sobre um qubit que se encontra no estado $\left|0\right\rangle$, esse qubit passará para o estado $\left|1\right\rangle$ e, quando a porta de Pauli X é aplicada sobre um qubit que se encontra no estado $\left|1\right\rangle$, esse qubit passará para o estado $\left|0\right\rangle$. A porta de Pauli X modifica o estado do qubit de modo que o novo estado terá $\alpha$ = $\beta_{0}$ e $\beta$ = $\alpha_{0}$, onde $\alpha_{0}$ e $\beta_{0}$ são as constantes complexas do estado anterior. A Figura 1 mostra as duas formas de representar a porta de Pauli X em circuitos quânticos.

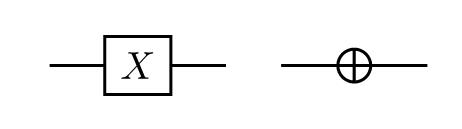
Figura 1. Representação em circuitos quânticos da porta de Pauli X.

O objetivo desse terceiro algoritmo é demonstrar o resultado da ação da porta de Pauli X. O algoritmo anterior foi desenvolvido para visualizar a ação da porta de Hadamard. Portanto, a única diferença do terceiro para o segundo algoritmo é a troca da porta de Hadamard pela porta de Pauli X. As verões do terceiro algoritmo para os SDKs Qiskit, Forest e Cirq são mostradas abaixo.

Qiskit

from qiskit import QuantumCircuit
from qiskit import QuantumRegister
from qiskit import ClassicalRegister
from qiskit import Aer
from qiskit import execute
qr = QuantumRegister(1)
cr = ClassicalRegister(1)
qc = QuantumCircuit(qr,cr)
qc.x(qr)
backend = Aer.get_backend ( 'statevector_simulator' )
job = execute(qc,backend)
resultado = job.result()
estado = resultado.get_statevector()
print(estado)

O estado inicial do qubit é $\left|0\right\rangle$ que corresponde a $\alpha$ = 1 e $\beta$ = 0. A ação da porta de Pauli X altera o estado do qubit para $\left|1\right\rangle$ que corresponde a $\alpha$ = 0 e $\beta$ = 1. O resultado da execução do algoritmo acima é [0. + 0.j 1. + 0.j], onde j é a unidade imaginária. Esse resultado indica que $\alpha$ = 0 e $\beta$ = 1, portanto o estado do qubit é $\left|1\right\rangle$ como esperado.

Forest

from pyquil import Program
from pyquil.gates import *
from pyquil.api import WavefunctionSimulator
p = Program()
p += X(0)
wf_sim = WavefunctionSimulator()
wavefunction = wf_sim.wavefunction(p)
print(wavefunction)
print(wavefunction.get_outcome_probs ())

O resultado desse algoritmo é:
(1 + 0j)$\left|1\right\rangle$
{'0': 0.0, '1': 1.0}

O coeficiente do estado $\left|1\right\rangle$ é $\beta$, portanto $\beta$ = 1 + 0j. Como o estado $\left|0\right\rangle$ foi omitido, o valor de $\alpha$ é 0. O método get_outcome_probs() retorna {'0': 0.0, '1': 1.0} que indica que a probabilidade de obter o resultado 0 é 0 e a probabilidade de obter o resultado 1 é 1.

Cirq

import cirq
qc = cirq.Circuit()
qr = cirq.NamedQubit('q[0]')
qc.append(cirq.X(qr))
simulador = cirq.Simulator()
resultado = simulador.simulate(qc)
print(resultado)

O resultado desse algoritmo é:
measurements: (no measurements)
output vector: $\left|1\right\rangle$

Não foi implementado medidor quântico no circuito para que uma medição fosse realizada. O circuito quântico foi simulado e, como resultado, o estado do qubit é fornecido. Esse estado é $\left|1\right\rangle$ devido à porta de Pauli X que alterou o estado do qubit de $\left|0\right\rangle$ para $\left|1\right\rangle$.