Algoritmo 1 – Qubit

Na página da Intel, os processadores i7 são especificados pela sua memória cache de 25 MB e pela sua frequência de 5.00 GHz. Essas são duas propriedades importantes para indicar o desempenho de um processador. Diferente de um processador clássico, um processador quântico tem o seu desempenho determinado pela quantidade de qubits que podem ser manipulados em uma operação. Então, fica a pergunta: o que seria um qubit?

Em um curso de programação de alguma linguagem de alto nível, é suficiente ao estudante saber que um bit é uma unidade que armazena informação, sendo que essa informação pode ser o valor 0 ou o valor 1. Pode-se também definir qubit como uma unidade que armazena informação, porém essa informação é um par de números complexos $\alpha$ e $\beta$ que satisfazem a condição $\left| \alpha \right|^2 + \left| \beta \right|^2 = 1$. Para obter o valor armazenado em um qubit realiza-se um processo chamado de medição. O resultado da medição de um qubit tem probabilidade $\left| \alpha \right|^2$ de ser 0 e probabilidade $\left| \beta \right|^2$ de ser 1. O qubit pode estar em dois estados diferentes ao mesmo tempo sendo que esses estados são identificados por $\left|0\right\rangle$ e $\left|1\right\rangle$. Essa notação pode parecer um pouco estranha ao estudante, mas preferiu-se manter essa notação por se tratar da notação utilizada para representar estados quânticos na física. O estudante está familiarizado com a notação {$\hat{x}$,$\hat{y}$} para representar a base de um espaço bidimensional. A base para representar o estado de um qubit é {$\left|0\right\rangle$,$\left|1\right\rangle$}. Essa base é conhecida como base computacional da computação quântica. O estado de um qubit é matematicamente descrito por:

$$ \left|\psi\right\rangle = \alpha \left|0\right\rangle + \beta \left|1\right\rangle. $$

O processo de medição interfere no estado do qubit de tal forma que, quando o resultado da medição é 0, o novo estado do qubit é $\left|0\right\rangle$ e, quando o resultado é 1, o novo estado do qubit é $\left|1\right\rangle$. Essa alteração no estado do qubit provocada pelo processo de medição é chamada de colapso de função de onda.

O primeiro algoritmo desse tutorial é dedicado a verificar essa importante propriedade de um qubit. Antes de iniciar nosso primeiro algoritmo, dois novos conceitos precisam ser introduzidos: circuito quântico e portas quânticas. Escrever um algoritmo quântico equivale a criar um circuito quântico. Portanto, um circuito quântico é uma forma de representar um algoritmo quântico. Um circuito quântico é composto por um conjunto de linhas horizontais sendo que cada linha está associada a um qubit que foi declarado no algoritmo. Algumas formas de representar circuitos quânticos pode incluir uma última linha horizontal dupla que corresponde ao conjunto de registradores clássicos onde os resultados das medições realizadas são armazenados.

As informações armazenadas em bits são manipuladas através de portas lógicas em um circuito digital. De modo análogo, as informações armazenadas em qubits são manipuladas através de portas quânticas em um circuito quântico. Cada porta quântica utilizada no circuito quântico é adicionada sobre a linha associada ao qubit em que a porta foi aplicada. A sequência das portas ao longo de cada linha obedece à ordem em que as portas são aplicadas. A Figura 1 mostra o circuito quântico associado ao primeiro algoritmo. Nesse circuito, utilizamos a porta de Hadamard que é representada por uma caixa com a letra H em seu interior. Essa porta quântica altera o estado do qubit sobre o qual ela é aplicada de modo que os valores $\left(\alpha + \beta \right)/\sqrt{2}$ e $\left(\alpha - \beta \right)/\sqrt{2}$ são atribuídos às variáveis $\alpha$ e $\beta$ do novo estado. Para realizar a medição do qubit, foi adicionado ao circuito um medidor quântico. Esse medidor é representado por uma caixa contendo o desenho de um indicador analógico.

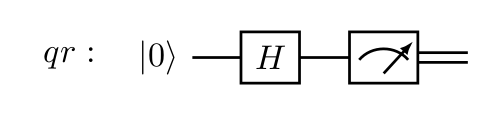
Figura 1. Circuito quântico correspondente ao algoritmo 1 desse tutorial.

Qiskit

As bibliotecas necessárias para esse primeiro algoritmo são: QuantumCircuit, QuantumRegister e ClassicalRegister. Essas bibliotecas devem ser importadas através das linhas de comando:
from qiskit import QuantumCircuit,
from qiskit import QuantumRegister
e
from qiskit import ClassicalRegister.
A biblioteca QuantumCircuit é necessária para criar o circuito quântico através do construtor QuantumCircuit(). A biblioteca QuantumRegister é necessária para instanciar o qubit utilizado no circuito quântico. Para isso, utiliza-se o construtor QuantumRegister(). Ao argumento, atribui-se o valor 1 porque será declarado apenas um qubit no circuito quântico. O valor obtido com a medição desse qubit deve ser armazenado em um registrado clássico que é instanciado pelo construtor ClassicalRegister() que também tem o valor 1 como argumento porque é necessário apenas 1 registrador para armazenar o resultado. Os argumentos do construtor QuantumCircuit() são os registradores quântico e clássico. Portanto, as linhas de comando que devem ser adicionadas ao programa são:
qr = QuantumRegister(1),
cr = ClassicalRegister(1)
e
qc = QuantumCircuit(qr,cr).

Os valores de $\alpha$ e $\beta$ para o qubit em seu estado inicial são 1 e 0, respectivamente. Portanto, a medição de um qubit em seu estado inicial sempre resultaria no valor 0. A ação da porta de Hadamard leva o qubit para um novo estado onde $\alpha = \left(1 + 0\right) / \sqrt{2} = 0,707$ e $\beta = \left(1 - 0\right) / \sqrt{2} = 0,707$. A medição desse qubit terá probabilidade 0,5 de resultar em 0 e, também, probabilidade 0,5 de resultar em 1. A porta de Hadamard é implementada por:
qc.h(qr).
A medição do qubit é feita com o método measure() para o qual passamos como argumento os registradores quântico e clássico. Logo, deve ser incluída no programa a linha de comando:
qc.measure(qr,cr).

A expressão backend refere-se ao sistema que executará o algoritmo. O método get_backend() é utilizado para selecionar esse sistema que pode ser um simulador ou um computador quântico. Esse método requer o framework Aer, portanto deve-se incluir entre as bibliotecas a serem importadas a linha de comando:
from qiskit import Aer.
O simulador é selecionado por:
backend = Aer.get_backend('qasm_simulator').
O algoritmo é executado pelo método execute() que requer, como argumentos, o circuito quântico que deve ser simulado e o sistema escolhido para executar o algoritmo. Pode-se também incluir, entre os argumentos, o número de execuções através do valor atribuído à variável shots. Se essa variável é omitida, então são realizadas 1000 execuções. Para realizar 100 execuções, a linha de comando que deve ser adicionada ao programa é:
job = execute(qc,backend,shots=100).
O método execute() requer a biblioteca execute. Logo, deve-se incluir entre as bibliotecas:
from qiskit import execute.
O resultado da execução é obtido com o uso do método result(). O método get_counts() é necessário para extrair do resultado a quantidade de medições que resultaram em 0 e a quantidade de medições que resultaram em 1. As linhas de comando que implementam esses métodos são:
resultado = job.result()
e
contagem = resultado.get_counts().
O resultado é impresso na tela pelo comando:
print(contagem).

O algoritmo completo é mostrado a seguir:

from qiskit import QuantumCircuit
from qiskit import QuantumRegister
from qiskit import ClassicalRegister
from qiskit import Aer
from qiskit import execute
qr = QuantumRegister(1)
cr = ClassicalRegister(1)
qc = QuantumCircuit(qr,cr)
qc.h(qr)
qc.measure(qr,cr)
backend = Aer.get_backend('qasm_simulator')
job = execute(qc,backend,shots=100)
resultado = job.result()
contagem = resultado.get_counts()
print(contagem)

Ao executar o algoritmo acima, pode-se obter, por exemplo, {'0': 60, '1': 40} que indica que o valor 0 foi obtido em 60 medições e o valor 1 foi obtido em 40 medições. Outro resultado possível seria {'0': 45, '1': 55}. Em cada medição há a probabilidade $\left| 1/\sqrt{2} \right|^2 = 0,5$ de que o resultado seja 0 e, também, a probabilidade $\left| 1/\sqrt{2} \right|^2 = 0,5$ de que o resultado seja 1. Se o valor 1 é atribuído à variável shots, os resultados possíveis seriam {'0': 1} ou {'1': 1} porque uma única medição é realizada.

Forest

Para escrever algoritmos quânticos com o SDK Forest, é preciso instanciar o objeto Program que requer a biblioteca Program. Portanto, pode-se começar o algoritmo com os comandos:
from pyquil import Program
e
p = Program().
Para implementar a porta de Hadamard, adiciona-se H(0) à variável p através de:
p += H(0).
O uso da porta de Hadamard requer que a biblioteca referente às portas quânticas seja adicionada ao programa por:
from pyquil.gates import *.
Para o processo de medição, é preciso declarar um bit com o método declare() por meio de:
ro = p.declare('ro', 'BIT', 1).
Esse método requer a biblioteca Declare que é acrescentada ao programa por:
from pyquil.quilbase import Declare.
Ao bit declarado, atribui-se um nome que, em nosso exemplo, foi ro. O medidor quântico pode ser adicionado ao circuito por:
p += MEASURE(0, ro[0]).

A quantidade de qubits que será manipulada pela máquina virtual quântica é definida pela função get_qc(). No algoritmo foi incluído o comando:
qc = get_qc("1q-qvm").
Esse comando define uma máquina virtual quântica de 1 qubit. Para uma máquina virtual quântica de 2 qubits, o argumento da função get_qc() seria "2q-qvm". O programa é compilado pelo método compile() e executado pelo método run(). Logo, para executar o algoritmo é preciso incluir as linhas de comando:
executable = qc.compile(p)
e
result = qc.run(executable).
Para imprimir no terminal somente os valores do resultado, pode-se adicionar o método readout_data.get(). Assim, acrescenta-se ao algoritmo:
print(result.readout_data.get( 'ro' )).
O algoritmo completo é mostrado abaixo.

from pyquil import get_qc, Program
from pyquil.gates import *
from pyquil.quilbase import Declare
p = Program()
p += H(0)
ro = p.declare('ro', 'BIT', 1)
p += MEASURE(0, ro[0])
qc = get_qc("1q-qvm")
executable = qc.compile(p)
result = qc.run(executable)
print(result.readout_data.get( 'ro' ))

Os resultados possíveis para esse algoritmo são: [ [0] ] e [ [1] ]. Isso porque a probabilidade de obter o resultado 0 é 0,5 e a probabilidade de obter o resultado 1 também é 0,5. Para aumentar o número de vezes que o algoritmo é executado, pode-se adicionar a linha de comando
p.wrap_in_numshots_loop(shots=10)
antes do comando para compilar o algoritmo. Nesse caso, um dos possíveis resultados seria:
[ [1]
  [1]
  [1]
  [0]
  [1]
  [0]
  [1]
  [0]
  [1]
  [1] ]
O resultado 0 foi obtido em três medições e o resultado 1 foi obtido em sete medições. O método wrap_in_numshots_loop() retorna uma matriz. Cada elemento dessa matriz é o resultado de uma medição. Funções da linguagem Python podem ser utilizadas para modificar a forma como o resultado é impresso.

Cirq

Com o SDK Cirq, uma única biblioteca é necessária para o primeiro algoritmo que é a biblioteca cirq. Assim, inicia-se o programa com:
import cirq.
No Cirq, qubits e outros objetos quânticos como circuitos quânticos são identificados por instâncias de subclasses. Logo, um circuito quântico é um objeto criado a partir de:
qc = cirq.Circuit().

Há três subclasses para instanciar qubits no SDK Cirq. Para identificar um qubit por uma string, usa-se cirq.NamedQubit(). A subclasse cirq.LineQubit() é utilizada para instanciar qubits em um vetor sendo que cada qubit é identificado por um índice. Para uma matriz de qubits, onde cada qubit é identificado por um par de índices, usa-se a subclasse cirq.GridQubit(). Assim, para instanciar o qubit a ser utilizado no algoritmo, pode-se adicionar a linha de comando:
qr = cirq.NamedQubit('q[0]').

A porta de Hadamard e o medidor quântico podem ser implementados no circuito quântico pelo método append(). As linhas de comando a serem adicionadas ao algoritmo são:
qc.append(cirq.H(qr))
e
qc.append(cirq.measure(qr)).
No Cirq, é suficiente instanciar um simulador com a subclasse cirq.Simulator() e executar o programa com o método run() que recebe a variável que identifica o circuito como argumento. Pode-se também incluir entre os argumentos do método run() a variável repetitions, que especifica o número de execuções do algoritmo, e atribuir um valor a essa variável. Assim, adiciona-se ao algoritmo:
simulador = cirq.Simulator(),
resultado = simulador.run(qc,repetitions=10)
e
print(resultado).

O algoritmo completo é mostrado abaixo.

import cirq
qc = cirq.Circuit()
qr = cirq.NamedQubit('q[0]')
qc.append(cirq.H(qr))
qc.append(cirq.measure(qr))
simulador = cirq.Simulator()
resultado = simulador.run(qc,repetitions=10)
print(resultado)

Em cada medição, é possível obter o resultado 0 ou o resultado 1. A probabilidade de obter o resultado 0 é 0,5 e a probabilidade de obter 1 é 0,5 conforme discutido anteriormente. Assim, um possível resultado para esse algoritmo é a sequência q[0]=1000100011 que indica que obteve-se seis vezes o valor 0 e quatro vezes o valor 1 nas dez medições realizadas. Outro possível resultado é q[0]=1101100001.