Algoritmo 5 – Porta CNOT

A porta de Hadamard e a porta de Pauli X são portas quânticas de um qubit. Nesse algoritmo, será implementado a porta CNOT que também é chamada de NOT-controlada. A Figura 1 mostra as duas formas de representação da porta CNOT em circuitos quânticos.

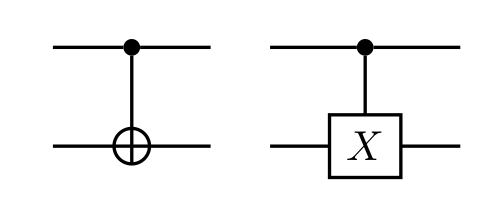
Figura 1. Formas de representação da porta CNOT em circuitos quânticos.

A porta CNOT atua em dois qubits onde o primeiro é chamado de qubit de controle e o segundo é chamado de qubit alvo. Se o qubit de controle encontra-se no estado $\left|1\right\rangle$, então o estado do qubit alvo é alterado de $\left|0\right\rangle$ para $\left|1\right\rangle$ ou de $\left|1\right\rangle$ para $\left|0\right\rangle$. Se o qubit de controle estiver no estado $\left|0\right\rangle$, o qubit alvo não sofre qualquer modificação. A porta CNOT pode ser comparada à porta lógica XOR porque o seu resultado pode ser representado por: $CNOT \left| a, b \right\rangle \rightarrow \left| a, a \oplus b \right\rangle$ onde $a$, $b$ $\in$ $\{0,1\}$. A Figura 2 mostra o circuito quântico a ser implementado no algoritmo 5 para permitir a visualização da ação da porta CNOT sobre o qubit alvo. Encontram-se abaixo as versões do algoritmo 5 para os SDKs Qiskit, Forest e Cirq.

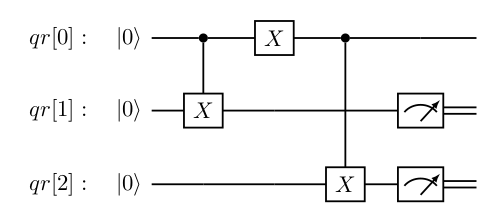
Figura 2. Circuito quântico referente ao algoritmo 5 desse tutorial.

Qiskit

Nas primeiras linhas do algoritmo, deve-se importar as bibliotecas necessárias que são as mesmas do primeiro algoritmo. O motivo do uso dessas bibliotecas é apresentado na discussão do algoritmo 1. Então, devem ser instanciados três qubits, dois registradores clássicos e o circuito quântico. As linhas de comando necessárias para instanciar esses objetos são:
qr = QuantumRegister(3),
cr = ClassicalRegister(2)
e
qc = QuantumCircuit(qr,cr).

No Qiskit, a porta CNOT é implementada pelo método cx() que recebe dois argumentos: o qubit de controle e o qubit alvo. A primeira porta CNOT é implementada por:
qc.cx(qr[0],qr[1]).
Essa porta é seguida por uma porta de Pauli X sobre o primeiro qubit que é implementada através de:
qc.x(qr[0]).
A segunda porta CNOT, que aparece após a porta de Pauli X, é implementada por:
qc.cx(qr[0],qr[2]).
Por fim, medidores quânticos sobre o segundo e o terceiro qubit são adicionados ao circuito. Nesse algoritmo será utilizado o simulador QASM Simulator sendo atribuído o valor de 100 para a variável shots para realizar 100 medições. Os comandos finais para a seleção do backend, a execução e a impressão dos resultados são explicadas no algoritmo 1. O algoritmo 5 completo para o SDK Qiskit é mostrado a seguir:

from qiskit import QuantumCircuit
from qiskit import QuantumRegister
from qiskit import ClassicalRegister
from qiskit import Aer
from qiskit import execute
qr = QuantumRegister(3)
cr = ClassicalRegister(3)
qc = QuantumCircuit(qr,cr)
qc.cx(qr[0],qr[1])
qc.x(qr[0])
qc.cx(qr[0],qr[2])
qc.measure(qr[1],cr[0])
qc.measure(qr[2],cr[1])
backend = Aer.get_backend('qasm_simulator')
job = execute(qc,backend,shots=100)
resultado = job.result()
contagem = resultado.get_counts()
print(contagem)

O resultado da execução do algoritmo acima é {'10': 100}. Em todas as medições realizadas, o resultado para o qubit qr[2] será sempre 1 e, para o qubit qr[1], sempre 0. A primeira porta CNOT não altera o estado do qubit qr[1] porque o estado do qubit de controle, que é o qubit qr[0], é $\left|0\right\rangle$. A segunda porta CNOT altera o estado de qr[2] para $\left|1\right\rangle$ porque o qubit de controle qr[0] teve o seu estado alterado para $\left|1\right\rangle$ pela porta de Pauli X anterior à segunda porta CNOT.

Forest

As bibliotecas utilizadas são aquelas utilizadas no algoritmo 1. O circuito quântico é instanciado por:
p = Program().
Os dois registradores clássicos necessários para armazenar os resultados das medições são instanciados por:
ro = p.declare('ro', 'BIT', 2).
A porta CNOT é implementada no circuito pelo método CNOT() que recebe como primeiro argumento o índice do qubit de controle e, como segundo argumento, o índice do qubit alvo. A primeira porta CNOT é implementada por:
p += CNOT(0,1).
Há a porta de Pauli X e, então, a segunda porta CNOT. Essas portas quânticas são implementadas por:
p += X(0)
e
p += CNOT(0,2).
Por fim, os medidores quânticos são implementados por:
p += MEASURE(1, ro[0])
e
p += MEASURE(2, ro[1]).
Uma máquina quântica virtual para simulação de sistemas com três qubits deve ser instanciada por:
qc = get_qc("3q-qvm").
O algoritmo completo é mostrado abaixo. As linhas de comando finais para a execução do algoritmo são discutidas no algoritmo 1.

from pyquil import get_qc, Program
from pyquil.gates import *
from pyquil.quilbase import Declare
p = Program()
ro = p.declare('ro', 'BIT', 2)
p += CNOT(0,1)
p += X(0)
p += CNOT(0,2)
p += MEASURE(1, ro[0])
p += MEASURE(2, ro[1])
qc = get_qc("3q-qvm")
executable = qc.compile(p)
result = qc.run(executable)
print(result.readout_data.get( 'ro' ))

A execução desse algoritmo resulta em [ [0 1] ]. O primeiro valor refere-se ao resultado da medição de qr[1] e o segundo, resultado da medição de qr[2]. A ordem em que esses valores são exibidos na tela do terminal é oposta à ordem em que os valores são exibidos com o uso do SDK Qiskit.

Cirq

O algoritmo inicia-se com o comando para importar a bilioteca cirq:
import cirq.
Então, o circuito quântico e os três qubits são instanciados por:
qc = cirq.Circuit(),
qr0 = cirq.NamedQubit('qr[0]'),
qr1 = cirq.NamedQubit('qr[1]')
e
qr2 = cirq.NamedQubit('qr[2]').
A primeira porta CNOT é adicionada ao circuito por:
qc.append(cirq.CNOT(qr0,qr1)).
Essa porta não altera o estado de qr[1] porque o estado de qr[0] é $\left|0\right\rangle$. A porta de Pauli X é adicionada ao circuito por:
qc.append(cirq.X(qr0)).
O qubit qr[0] tem o seu estado alterado para $\left|1\right\rangle$. A segunda porta CNOT é implementada por:
qc.append(cirq.CNOT(qr0,qr2)).
Essa porta altera o estado de qr[3] para $\left|1\right\rangle$ porque, agora, o estado de qr[0] é $\left|1\right\rangle$. Os medidores quânticos foram adicionados por:
qc.append(cirq.measure(qr1,key = 'qr[1]'))
e
qc.append(cirq.measure(qr2,key = 'qr[2]')).
O simulador foi instanciado e o programa executado com o método run(). O algoritmo 5 para o SDK Cirq fica:

import cirq
qc = cirq.Circuit()
qr0 = cirq.NamedQubit('qr[0]')
qr1 = cirq.NamedQubit('qr[1]')
qr2 = cirq.NamedQubit('qr[2]')
qc.append(cirq.CNOT(qr0,qr1))
qc.append(cirq.X(qr0))
qc.append(cirq.CNOT(qr0,qr2))
qc.append(cirq.measure(qr1,key = 'qr[1]'))
qc.append(cirq.measure(qr2,key = 'qr[2]'))
simulador = cirq.Simulator()
resultado = simulador.run(qc,repetitions=10)
print(resultado)

O resultado da execução é:
qr[1]=0000000000
qr[2]=1111111111

Como nos algoritmos anteriores, o resultado da medição do qubit qr[1] é 0 e do qubit qr[2] é 1 em todas as medições realizadas. No resultado acima, temos dez valores 0 para o qubit qr[1] e dez valores 1 para o qubit qr[2] que correspondem às dez medições realizadas que é resultado da atribuição do valor 10 à variável repetitions.